top of page
csx-home>vol-01>issue-01>CMOS + stochastic nanomagnets: heterogeneous computers for probabilistic inference and learning
Locked Premium
Submitted 16 March 2023
Revised 10 April 2023
Accepted 17 April 2023
CMOS + stochastic nanomagnets: heterogeneous computers for probabilistic inference and
learning
Keito Kobayashi
Nihal Singh
Qixuan Cao
Kemal Selcuk
1 Tianrui Hu,1 Shaila Niazi,1 Navid Anjum
Aadit,1 Shun Kanai,2, 3, 4, 5, 6, 7, 8 Hideo Ohno,2, 4, 5, 9 Shunsuke Fukami,2, 3, 4, 5, 9, 10, †
and Kerem Y. Camsari1, ‡
Canadian Science Letters X
2023 ° 21(04) ° 01-01
https://www.wikipt.org/csx-home
DOI: 10.1490/6576987.621csx
Funding Agent Details
Not Applicable.
Abstract
Extending Moore’s law by augmenting complementary-metal-oxide
semiconductor (CMOS) transistors with emerging nanotechnologies (X) has become increasingly important. Accelerating Monte Carlo algorithms that rely on random sampling with such CMOS+X technologies could have signicant impact on a large number of elds from probabilistic machine learning, optimization to quantum simulation. In this paper, we show the combination of stochastic magnetic tunnel junction (sMTJ)-based probabilistic bits (p-bits) with versatile Field Programmable Gate Arrays (FPGA) to design a CMOS + X (X = sMTJ) prototype. Our approach enables high-quality true randomness that is essential for Monte Carlo based probabilistic sampling and learning. Our heterogeneous computer successfully performs probabilistic inference and asynchronous Boltzmann learning, despite device-to-device variations in sMTJs. A comprehensive comparison using a CMOS predictive process design kit (PDK) reveals that compact sMTJ-based p-bits replace 10,000 transistors while dissipating two orders of magnitude of less energy (2 fJ per random bit), compared to digital CMOS p-bits. Scaled and integrated versions of our CMOS + stochastic nanomagnet approach can signicantly advance probabilistic computing and its applications in various domains by providing massively parallel and truly random numbers with extremely high throughput and energy-eciency.
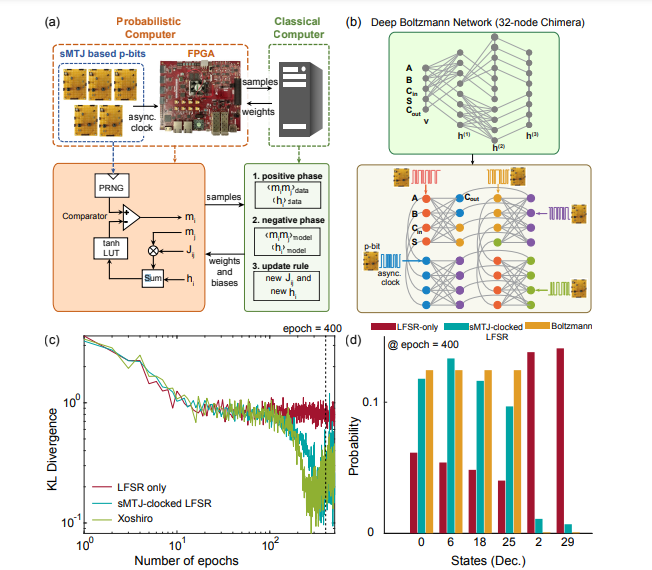
Introduction
With the slowing down of Moore’s Law [1], there has been a growing interest in domain-specific hardware and architectures to address emerging computational challenges and energy-efficiency, particularly borne out of machine learning and AI applications. One promising approach is the co-integration of traditional complementary metaloxide semiconductor (CMOS) technology with emerging nanotechnologies (X), resulting in CMOS + X architectures. the primary objective of this approach is to augment existing CMOS technology with novel functionalities, enabling the development of energy-ecient hardware systems that can be applied to a wide range of problems across various domains. By blending CMOS with alternative materials and devices, CMOS + X architectures can enhance traditional CMOS technologies in terms of energy-efficiency and performance Being named one of the top 10 algorithms of the 20th century [2], Monte Carlo methods have been one of the most ∗ ese authors contributed equally effective approaches in computing to solve computationally hard problems in a wide range of applications, from probabilistic machine learning, optimization to quantum simulation. Probabilistic computing with p-bits [3] has emerged as a powerful platform for executing these Monte Carlo algorithms in massively parallel [4, 5] and energy efficient architectures. p-bits have been shown to be applicable to a large domain of computational problems from combinatorial optimization to probabilistic machine learning and quantum simulation [6–8]. Several p-bit implementations that use the inherent stochasticity in different materials and devices have been proposed, based on diusive memristors [9], resistive RAM [10], perovskite nickelates [11], ferroelectric transistors [12], single photon avalanche diodes [13], optical parametric oscillators [14] and others. Among alternatives sMTJs built out of low-barrier nanomagnets have demonstrated signicant potential due to their ability to amplify noise, converting millivolts of uctuations to hundreds of millivolts over resistive networks [15], unlike alternative approaches with amplifiers [16]. Another advantage of sMTJ-based pbits is the continuous generation of truly random bitstreams without the need to be reset in synchronous pulsebased designs [17, 18]. The possibility of designing energy-efficient p-bits using low-barrier nanomagnets has ...............Read more by purchasing the full lenghth.
Conclusion
This work demonstrates the first hardware demonstration of a heterogeneous computer combining versatile FPGAs with stochastic MTJs for probabilistic machine learning and inference. We introduce a new variation tolerant pbit circuit that is used to create an asynchronous clock domain, driving digital p-bits in the FPGA. In the process, the CMOS + sMTJ computer shows how commonly used and inexpensive PRNGs can be augmented by magnetic nanodevices to perform as well as high quality PRNGs, both in probabilistic inference and learning experiments. Our CMOS + sMTJ computer also shows the first demonstration of training a deep Boltzmann network in a 32-node Chimera topology, leveraging the asynchronous dynamics of sMTJs. Careful comparisons with existing digital circuits show the true potential of integrated sMTJs which can be scaled up to million p-bit densities far beyond the capabilities of present day CMOS technology.
References
[1] omas N eis and H-S Philip Wong. e end of moore’s law: A new beginning for information technology. Computing in Science & Engineering, 19(2):41–50, 2017.
[2] Jack Dongarra and Francis Sullivan. Guest editors introduction to the top 10 algorithms. Computing in Science & Engineering, 2(01):22–23, 2000.
[3] K. Y. Camsari et al. Stochastic p-bits for invertible logic. Physical Review X, 7(3):031014, 2017.
[4] Brian Suon et al. Autonomous probabilistic coprocessing with petaips per second. IEEE Access, 8:157238–157252, 2020.
[5] Navid Anjum Aadit, Andrea Grimaldi, Mario Carpentieri, Luke eogarajan, John M Martinis, Giovanni Finocchio, and Kerem Y Camsari. Massively parallel probabilistic computing with sparse ising machines. Nature Electronics, pages 1–9, 2022.
[6] Jan Kaiser and Supriyo Daa. Probabilistic computing with p-bits. Applied Physics Leers, 119(15):150503, 2021.
[7] Kerem Y Camsari, Brian M Suon, and Supriyo Daa. P-bits for probabilistic spin logic. Applied Physics Reviews, 6(1):011305, 2019.
[8] Shuvro Chowdhury, Andrea Grimaldi, Navid Anjum Aadit, Shaila Niazi, Masoud Mohseni, Shun Kanai, Hideo Ohno, Shunsuke Fukami, Luke eogarajan, Giovanni Finocchio, et al. A full-stack view of probabilistic computing with pbits: devices, architectures and algorithms. IEEE Journal on Exploratory Solid-State Computational Devices and Circuits, 2023.
[9] Kyung Seok Woo, Jaehyun Kim, Janguk Han, Woohyun Kim, Yoon Ho Jang, and Cheol Seong Hwang. Probabilistic computing using cu0. 1te0. 9/hfo2/pt diusive memristors. Nature Communications, 13(1):5762, 2022.
[10] Yixuan Liu, Qiao Hu, Qiqiao Wu, Xuanzhi Liu, Yulin Zhao, Donglin Zhang, Zhongze Han, Jinhui Cheng, Qingting Ding, Yongkang Han, et al. Probabilistic circuit implementation based on p-bits using the intrinsic random property of rram and p-bit multiplexing strategy. Micromachines, 13(6):924, 2022. [11] Tae Joon Park, Kemal Selcuk, Hai-Tian Zhang, Sukriti Manna, Rohit Batra, Qi Wang, Haoming Yu, Navid Anjum Aadit, Subramanian KRS Sankaranarayanan, Hua Zhou, et al. Ecient probabilistic computing with stochastic perovskite nickelates. Nano Leers, 22(21):8654–8661, 2022.
[12] Sheng Luo, Yihan He, Baofang Cai, Xiao Gong, and Gengchiau Liang. Probabilistic-bits based on ferroelectric eld-eect transistors for stochastic computing. arXiv preprint arXiv:2302.02305, 2023.
[13] William Whitehead, Zachary Nelson, Kerem Y Camsari, and Luke eogarajan. Cmos-compatible ising and pos annealing using single photon avalanche diodes. arXiv preprint arXiv:2211.12607, 2022.
[14] Charles Roques-Carmes, Yannick Salamin, Jamison Sloan, Seou Choi, Gustavo Velez, Ethan Koskas, Nicholas Rivera, Steven E Kooi, John D Joannopoulos, and Marin Soljacic. Biasing the quantum vacuum to control macroscopic probability distributions. arXiv preprint arXiv:2303.03455, 2023.
[15] Kerem Yunus Camsari, Sayeef Salahuddin, and Supriyo Daa. Implementing p-bits with embedded mtj. IEEE Electron Device Leers, 38(12):1767–1770, 2017.
[16] Suresh Cheemalavagu, Pinar Korkmaz, Krishna V Palem, Bilge ES Akgul, and Lakshmi N Chakrapani. A probabilistic cmos switch and its realization by exploiting noise. In IFIP International Conference on VLSI, pages 535–541, 2005.
[17] Akio Fukushima, Takayuki Seki, Kay Yakushiji, Hitoshi Kubota, Hiroshi Imamura, Shinji Yuasa, and Koji Ando. Spin dice: A scalable truly random number generator based on spintronics. Applied Physics Express, 7(8):083001, 2014.
[18] Laura Rehm, Corrado Carlo Maria Capriata, Misra Shashank, J Darby Smith, Mustafa Pinarbasi, B Gunnar Malm, and Andrew D Kent. Stochastic magnetic actuated random transducer devices based on perpendicular magnetic tunnel junctions. arXiv preprint arXiv:2209.01480, 2022.
[19] Christopher Safranski, Jan Kaiser, Philip Trouilloud, Pouya Hashemi, Guohan Hu, and Jonathan Z Sun. Demonstration of nanosecond operation in stochastic magnetic tunnel junctions. Nano Leers, 21(5):2040–2045, 2021.
[20] Keisuke Hayakawa, Shun Kanai, Takuya Funatsu, Junta Igarashi, Butsurin Jinnai, WA Borders, H Ohno, and S Fukami. Nanosecond random telegraph noise in in-plane magnetic tunnel junctions. Physical Review Leers, 126(11):117202, 2021.
[21] Leo Schnitzspan, Mathias Klaui, and Gerhard Jakob. ¨ Nanosecond true random number generation with superparamagnetic tunnel junctions–identication of joule heating and spin-transfer-torque eects. arXiv preprint arXiv:2301.05694, 2023.
[22] Jan Kaiser, Avinash Rustagi, Kerem Y Camsari, Jonathan Z Sun, Supriyo Daa, and Pramey Upadhyaya. Subnanosecond uctuations in low-barrier nanomagnets. Physical Review Applied, 12(5):054056, 2019.
[23] Orchi Hassan, Rafatul Faria, Kerem Yunus Camsari, Jonathan Z Sun, and Supriyo Daa. Low-barrier magnet design for ecient hardware binary stochastic neurons. IEEE Magnetics Leers, 10:1–5, 2019.
[24] Shun Kanai, Keisuke Hayakawa, Hideo Ohno, and Shunsuke Fukami. eory of relaxation time of stochastic nanomagnets. Physical Review B, 103(9):094423, 2021.
[25] Takuya Funatsu, Shun Kanai, Jun’ichi Ieda, Shunsuke Fukami, and Hideo Ohno. Local bifurcation with spin-transfer torque in superparamagnetic tunnel junctions. Nature communications, 13(1):4079, 2022.
[26] Kerem Y Camsari, Mustafa Mert Torunbalci, William A Borders, Hideo Ohno, and Shunsuke Fukami. Double-freelayer magnetic tunnel junctions for probabilistic bits. Physical Review Applied.
[27] Keito Kobayashi, Keisuke Hayakawa, Junta Igarashi, William A Borders, Shun Kanai, Hideo Ohno, and Shunsuke Fukami. External-eld-robust stochastic magnetic tunnel junctions using a free layer with synthetic antiferromagnetic coupling. Physical Review Applied, 18(5):054085, 2022.
[28] William A Borders et al. Integer factorization using stochastic magnetic tunnel junctions. Nature, 2019.
[29] Jan Kaiser, William A Borders, Kerem Y Camsari, Shunsuke Fukami, Hideo Ohno, and Supriyo Daa. Hardware-aware in situ learning based on stochastic magnetic tunnel junctions. Physical Review Applied, 17(1):014016, 2022.
[30] Damir Vodenicarevic, Nicolas Locatelli, Alice Mizrahi, Joseph S Friedman, Adrien F Vincent, Miguel Romera, Akio Fukushima, Kay Yakushiji, Hitoshi Kubota, Shinji Yuasa, et al. Low-energy.
............
bottom of page




















